What?!
In the year 300 BC Aristotle discovered what became known as The Wheel Paradox. If two circles of a differing diameters (the small circle being contained within the large circle) both have a line constrained to a circumferential node on the Y axis, and these wheels are then rotated [see figure 1], the lengths of the two parallel lines are equal. This caused Aristotle’s head to ache, and after a few wines to clear up the image… His head ached even more.
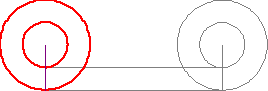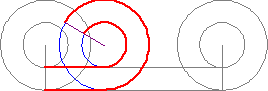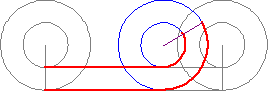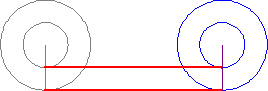
The only logical conclusion Aristotle was able to draw from this, was that the circumferences of the circles had to be the same; “makes sense” is what we assume he said. But not quite, it can be hypothesised that inebriated in his local tavern Aristotle described this whole affair as “a melon twister, Geoff”.
Solving the melon twister
Fast forward nearly 2,000 years (about how long it feels reading this), and in his final works Italian astronomer, engineer, physicist and jack of all trades Galileo solves it. He applied some askew thinking and recreated the two-circle thought experiment, but rather than using circles, he drew hexagons [see figure 2]. What a crazy dude, right? They’re not the same things. Well, not really - his vision corrected the paradox.

The flat side AB is the hexagon’s starting position; if the hexagon is then rotated, pivoting on point B, its second position will be on the flat side BC. This BC flat will now be located on position SB to SQ along the straight line. This will repeat all the way to the end. Simples!
Now the inner hexagon, this one’s more of a renegade. Its starting position is the flat side HI, and when rotated (whilst remaining constrained concentric to the outer hexagon), the flat side IK will skip the line location TI and TO, leapfrogging to the line position TO and TP.
You get all that? if not, try looking at figures 3 and 4; this may help.


With this understanding, Galileo then had to determine how this approach could be applied to circles, and the answer was: infinity. He developed the understanding that if the number of sides increases from 6 to 8, and then from 8 to 10, then the flat sides would decrease in size and the shape would become more rounded. Now let’s scale it up, if we imagine (with Galileo) a polygon with 100,000 thousand flat sides, the shape would appear round, but the underpinning principle discussed above would still apply. So, let’s understand a circle: if we define it as having an infinite number of nodal points and flat sides, we can confirm that two circles of differing diameters do not have the same circumference and are in fact different sizes, and that the answer was infinity.
Triangles
Where do triangles come in? If we’re to understand 2D geometry, any flat sided shape contains angles; any time an angle is present within geometry there are automatically two sides. If a third side is added, then this becomes a triangle. When the above is understood, then we can also consider circles to be constructed from triangles. So that takes care of 2D geometrical shapes in an X and Y setting; but to make things be things we need to a third dimension, the Z axis. Automatically by creating this 3rd dimension, an angle is created, thus (yes, we used the word thus) meaning that on the Z plane the 3D construct is also a triangle.
So how does all this relate to engineering? Well, we are a part of the science world and these fundamental principles assist with the governance of items such as flight trajectory, space engineering, torque load systems on an everyday basis.
WOW! That was a journey, we hope you enjoyed it and maybe learned something new. Remember - engineering is science 😊
